TA的每日心情 | 开心
2021-5-6 09:30 |
|---|
签到天数: 1 天 [LV.1]九品 酒贼
超级版主
- 积分
- 7499
|
最近在抖音上看到一个视频：一个大爷在街上摆摊，用一个袋子装了红绿蓝各8个珠子。玩家把手伸进口袋摸出12个珠子，数出不同颜色珠子个数，就能够获得相应的奖金。 . b, l# K* `% {- j* X
# H0 [% m& B# X( g6 y0 K' a
% H7 d: q& C+ K- K+ B' @& s. o0 s: r+ `! C
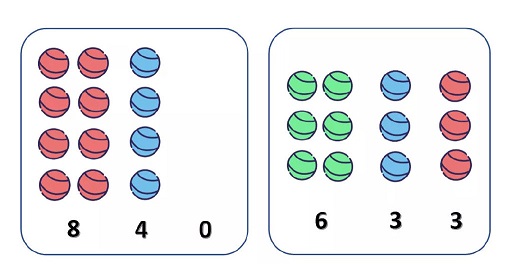
比如摸出的12个珠子里，颜色最多的珠子有8个，颜色次多的珠子有4个，还有一种颜色没有，就叫840，玩家会获得100元！如果珠子个数是831，就能获得10元，如果是444，就能获得1元等等。
9 R' k+ [, D7 e7 r4 |1 k" U7 _6 b7 T* o, s% \4 r. A. e
" f5 w) f; A! b* L
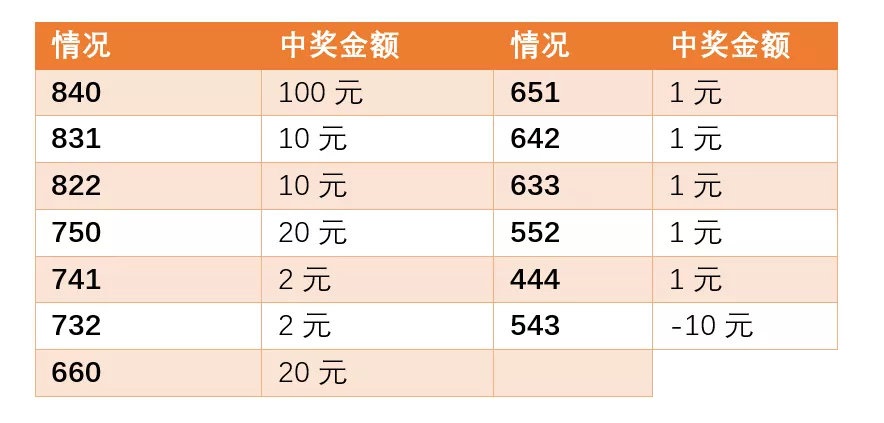
2 h5 P+ p% w5 H, p! J 但是还有一种情况，如果三种颜色珠子的个数是543，玩家还得给老板10元。全部的情况和中奖金额如下：) b2 M* T4 C' h* F, B0 `
( _0 p/ Q- E2 z% Z6 ~
0 V0 g3 J8 {% Y# w L! U4 D ]' ^; f L6 b6 f: i" v
这个游戏看起来赢面很大——13种情况中12种都挣钱，只有一种输钱。可是这个小朋友玩了好几次，还把自己的亲戚朋友都叫来玩，结果一直输钱，这是为什么呢？
9 ^! e% h# F1 ~ E
- Q6 @1 n6 g3 {% l; G9 U 很显然，这是一个概率游戏。我们首先要计算从24个珠子中摸出12个珠子一共有多少种可能，然后再计算每一种中奖的情况对应多少种可能，就能计算中奖的概率了。
4 w) k! A9 k) b7 u3 |2 P- X0 l9 H+ n0 ~" q# z
一.总共的情况数
( [6 S0 P$ {/ o( D- Y6 Y
! S: f! F4 u8 G& P0 k 从n个元素里取出m个元素的方法数叫做组合数，数学告诉我们： , `! z0 F% H7 A
- j! a b9 Q/ Y, t1 x 一共有24个球，取出12个，按照组合数公式 3 ^( j9 [8 ?: A9 h) R* p/ T
7 M7 z: ~. `! v, T n, Z 即从袋子中取出的球，不计算先后次序，一共有二百七十万四千一百五十六种情况。
8 x0 V1 u3 _: I- M# O: H. B8 j o- T( H
二.中奖的情况数+ r: n O$ X, {2 C, }0 {! {
# M( u) w+ i0 L( M
我们需要把中奖的情况分为三类：三个数字不同、两个数字相同、三个数字都相同。
$ y5 m$ m! G$ ] Y' Y
5 k, n/ h9 f/ c8 e$ p Y! ^! h 01三个数字不同
0 M! ?5 v/ c" G4 O
, D$ @2 F+ }$ v. a( t 如果取出三种颜色的球数量彼此不同，比如840这样的情况，首先要区分红、绿、蓝三种颜色的球，谁最多，谁其次，谁最少。对颜色进行排序有6种可能，分别是红绿蓝、红蓝绿、绿红蓝、绿蓝红、蓝红绿、蓝绿红。 ]& {, c( i4 k* ^' c
' S( j3 V9 V# N
然后，在第一种颜色的8个球中取8个，第二种颜的8个球中取4个，第三种颜色的8个球中取0个，所以840对应的情况数是：
5 F: T9 Z# g, y! {% ~8 M
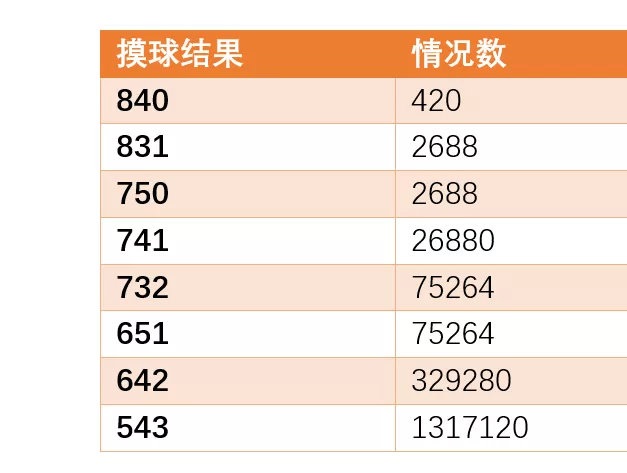
; P0 z7 E/ x2 g! r$ F( e 类似的，我们可以计算出其他几种结果的情况数：
# M1 ` E8 F& e# [3 M' v% q( t' G; R* C" D/ C6 {: ]
$ z' s6 {- k8 v
9 g: j; r$ H7 ]$ r/ `3 C 02两个数字相同3 D, Q. ~/ r0 e, b. E1 U1 r
* ?3 M8 h; A3 }8 ~$ K
如果取出的的球，有两种球个数一样多，比如822，又该怎么计算呢？% E5 Q/ I: R6 U- y C
9 ^& [) E0 n1 Z
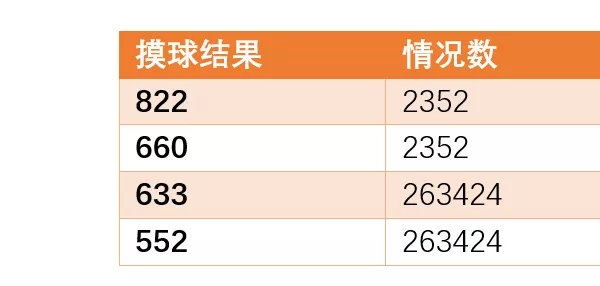
这时，首先要在三种颜色中选出一种，让它的个数与另外两种不同，比如红色、绿色、蓝色哪种颜色有8个球？这有三种情况。确定了个数不同的球的颜色，另外两个颜色的球个数相同，就不用区分了。你应该能计算出822这种结果对应的情况数
" r( U, `+ Y5 k4 ~; B4 J' k: K
+ @( B K$ ]( u$ w) z/ V
7 N8 y' s" E0 b# y. B5 Q5 [5 T( C( w
6 {% q l' a7 ^/ o) E 03三个数字相同8 e ]- n1 n4 g4 c+ E e* S8 H# V
! z$ q# n$ H7 @! G0 z 如果摸出12个球，每种颜色各有4个，就属于第三种情况。这时我们不需要再对颜色排序，只需要从每种颜色的8个球中取出4个即可，方法数有：
# G: c4 D/ _" v2 a" j
! j7 ^, L4 k% E$ D- t9 `, x
& [; S4 t$ w+ K' w. `0 T6 ~4 _( d0 C" }7 O4 w! V' c% g
三. 概率和期望/ O# {, X3 m. }6 ] m7 C; y
- S; P0 H- j+ Y- n9 r- o% h
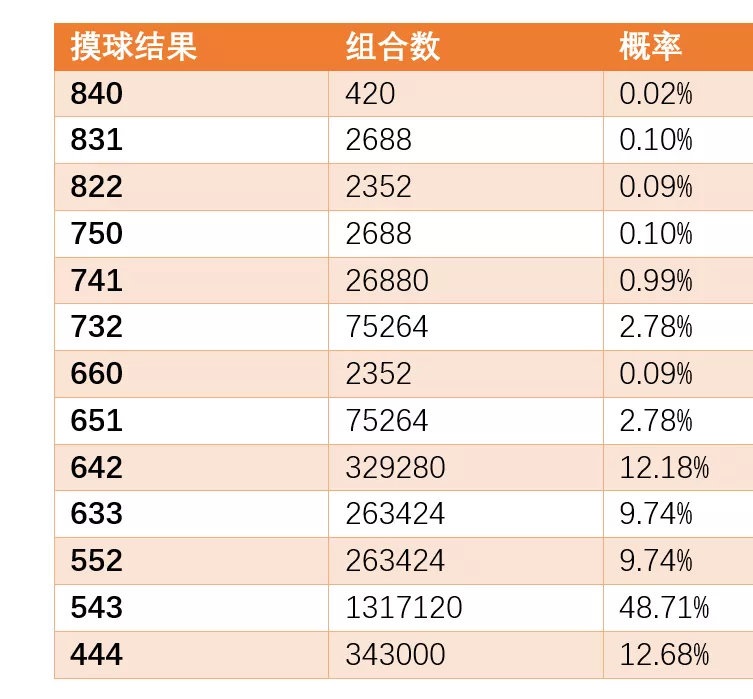
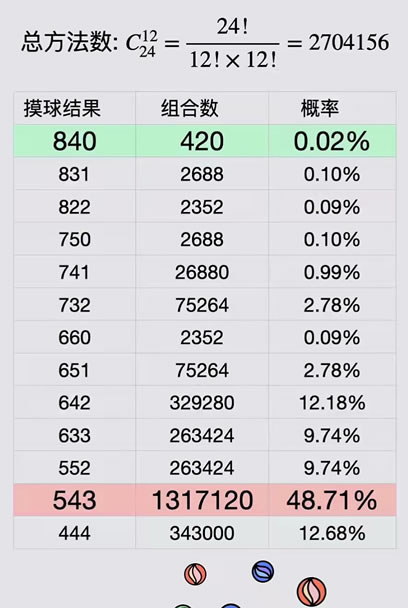
从24个球中摸出12个，共有2704156种方法。13种中奖的可能，每一种对应的情况数从420种到1317120不等。某种结果的情况数越多，出现的概率越大，概率等于这种结果的情况数除以24个球中摸出12个总的情况数： : _* ?9 o! X/ E" v9 i
. b9 d0 `+ ~; L( J" B
你会发现：概率最大的结果是543，概率48.7%，概率最小的结果是840，只有0.02%的可能。几乎玩2把就有一把是543，玩5000把才会出现一把840!' e4 h" v$ L" x. h
+ @, E' i% x P& U+ e8 b2 e 不同的情况，获得的奖金不同。用概率乘以对应情况的奖金，就得到了期望。所谓期望，就是这种获奖规则下平均能够给玩家的回报。3 N6 k) x `- L) T* n
U: k9 }2 I: |8 b
5 f1 ^5 D5 i, V5 g% a
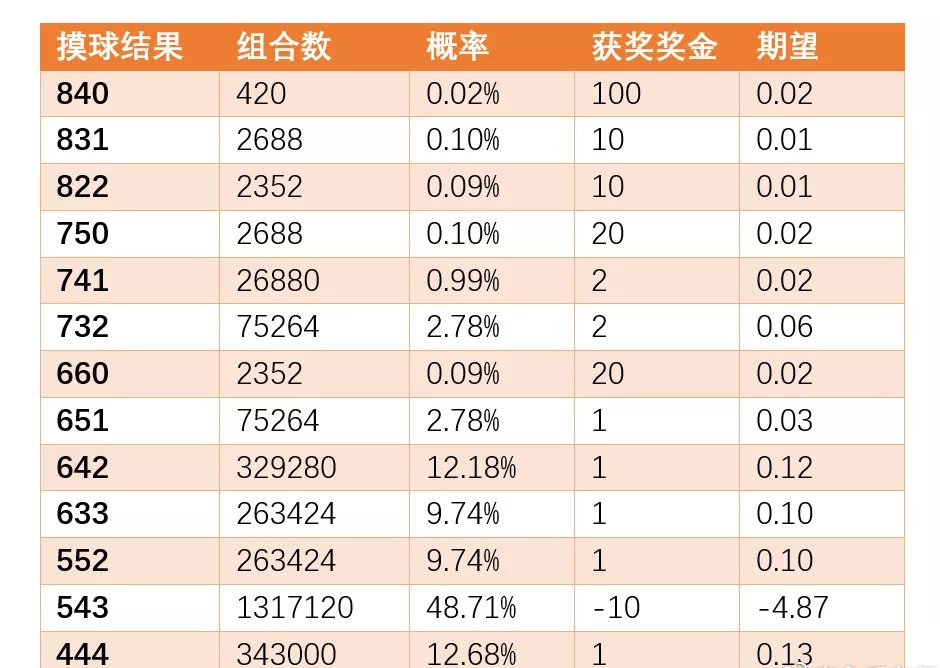
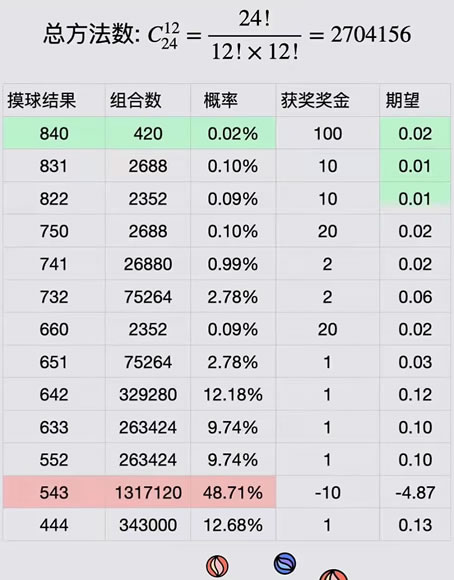
, F# s6 e w/ @4 I/ G+ F$ }% J8 p' h3 ^0 }4 | 我们把表格补充完整：
/ ?1 V( G) v8 s+ X9 @! m( G. ^/ j1 ]; U1 O3 S
1 V& q# o) \/ s6 O5 t' o+ X
$ k3 N$ d9 r$ v& b9 p8 T4 U 你发现了什么吗？赢钱的结果有12种，但是每一种情况下赢钱的期望都是几分钱到一毛多。输钱的结果只有543一种，但是这一种情况的期望却是-4.87元！把所有结果的期望相加，就会得到这个游戏的总期望值：-4.25元！每次玩游戏，玩家平均输掉4.25元！
! g) ?; ?0 E6 C3 e; L- ^
/ u" x5 I( f6 [/ I* M! U) r 敢开饭店就不怕大肚汉，敢街头摆摊就不怕你来玩。想从大爷手里挣钱，你还是太天真了！
" [& k/ Q: _! A3 `9 v8 a! M' M
0 ^% ^$ H& N! o/ ?
" e% W1 H6 z7 b4 a5 ^
|
|
发表于 2022-2-9 14:59:22
